FUNCIONES

 FUNCIONES

Dados dos conjuntos no vacíos A y B, una función ƒ de A en B, que se escribe.ƒ : A→B y se lee "ƒ" es una función o aplicación de A en B", es un subconjunto de AxB tal que todo xЄA está relacionado a un solo elemento yЄB. Es decir, en una función no se tienen dos pares ordenados distintos con la misma primera componente. Así, pues, toda función ƒes una relación especial de A en B.

Dado un par (x, y) Є ƒse escribe V= ƒ (x) y se dice que y es la imagen de x por ƒ, o que y es el valor de ƒen x, o bien que ƒ transforma x en y.

DEFINICIÓN

ƒ es una funcion o aplicación de A en B si y solo si ƒ es una relación entre A y B, que satisface las siguientes condiciones:

 COMPOSICIÓN DE FUNCIONES

Searr ƒ: A → B v g: B → C dos funciones tales que cl codominio de ƒ coincidc con el dominio de g (o bien I(ƒ) = D(g)): puede entonces definirse una nueva funcion g  ƒ de A en C llamada función cornpuesta de ƒ y g . como se muestra en el siguiente diagrama:

 

CLASIFICACIÓN DE FUNCIONES

FUNCIÓN INYECTIVA

Sea ƒ: A en B una función dice que ƒ es inyectiva o uno si cada elemento y e B es imagen de un  solo elemento x Є A. Es decir:

FUNCIÓN SOBREYECTIVA

Se dice que ƒ es una funcion sobreyectiva si y solo si todo elemento del codominio B es imagen de por lo menos  de un elemento  de A. Esto significa que ƒ es sobreyectiva cuando el conjunto de imagenes es B. así. se define

FUNCIÓN BIYECTIVA

Se dice que ƒ es una función biyectiva, si ƒ es inyectiva o sobreyectiva ( o una correspondencia biunívoca entre A y B) esto significa que para todo y e B hay exactamente un solo x Є tal que ƒ(x)=y. Es decir.

FUNCIONES INVERSAS

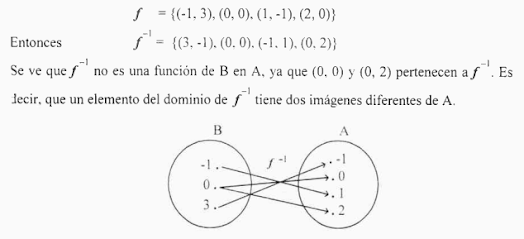
Toda funcion ƒ : A →B es una relación inversa ƒ-1 es un conjunto bien definido BxA, sin embargo ƒ-1 no es necesariamente una funcion  de B en A por ejemplo sean A= {-1,0,1,2} B={-1,0,3} y sea ƒ: A → B una funcion tal que ƒ(x) = x² al cuadrado -2x, es decir.

FUNCIÓN IDENTIDAD

La función que asigna a cada elemento de A el mismo elemento, se llama función identidad en A. Es decir. IA:A → A talque IA(x)=x

PROPIEDADES

Sea F : A es B  una funcion cualquiera y sean intermedio: A es A y la B es B las funciones identidad en A y en B, respectivamente. Entonces se tiene