CONJUNTOS

INTRODUCCIÓN A CONJUNTOS

Conceptos basicos de la teoría intuitiva de conjuntos, notaciones, subconjuntos, sus operaciones y sus aplicaciones. Para alcanzar los fines prácticos que nos interesan se completa con bastante cantidad de ejemplos ilustrativos.

1. CONCEPTO Y NOTACIÓN DE CONJUNTOS

En el lenguaje corriente, empleamos el vocablo conjunto para referirnos a una pluralidad o colectividad de objetos que se consideran agrupados formando un todo. Por ejemplo, conjunto de alumnos de una clase; conjunto de letras del abecedario; conjunto de escritores nacionales, etc.

De esta noción de pluralidad contrapuesta a la de singularidad ha surgido el concepto matemático de conjunto. Los ejemplos recién mencionados bastan por ahora para tener una idea de dicho concepto. Lo esencial de dichas situaciones es la presencia de elementos o miembros del conjunto, los mismos se les denota usualmente por letras minúsculas como a, b, c,..., y los conjuntos se denotan por lo común mediante letras mayúsculas como A, B, C, ....

Otros símbolos de uso frecuente son:

" / " para expresar "tal que"

" Є " pafa expresar que un elemento "pertenece" a un conjunto.

" < " para expresar "menor que".

" > " para expresar "mayor que"

EJEMPLO:

1.1 NOTACIÓN DE CONJUNTOS NUMÉRICOS

-Conjuntos de los números naturales N ={ 1,2,3,4,5,........}

-Conjuntos de los números enteros Z ={.....,-2,-1,0,1,2,3,.......}

-Conjuntos de los números racionales Q ={....,-3/5,2/3,0,1,2,....}

-Conjuntos de los números irracionales I={.....,√2,pi,e,√3,....}

-Conjutnos de los números reales R ={Q,I}

2. DETERMINACIÓN DE UN CONJUNTO

2.1 Por extension; Se dice que un conjunto está determinado por extensión sí y solo sí se nombran todos los elementos que lo constituyen. En este caso se escriben sus elementos entrp dos llaves.

2.2 Por conprension; Se dice que un conjunto está determinado por comprensión sí y solo si se da la propiedad o propiedades que caracterizan a todos los elementos del conjunto.

3. CONJUNTOS ESPECIALES

Llamaremos conjuntos especiales a aquellos conjuntos que se caracterizan por el número de elementos, entre ellos tenemos: conjunto unitario, conjunto vacío, conjunto universal.

3.1 CONJUNTO UNITARIO

Es aquel conjunto que tiene un sólo elemento.

3.2 CONJUNTO VACIO

El conjunto nulo o vacío es aquél conjunto que carece de elementos, y se denota por este simbolo Ф o por este { }

3.3 CONJUNTO UNIVERSAL

El conjunto universal, llamado también universo o referencial, es un conjunto de cuyos elementos se escogen algunos de ellos para formar otros conjuntos. Se denota por U.

4. RELACIONES ENTRE CONJUNTOS

Se sabe que el símbolo Є (pertenencia) se utiliza para relacionar un elemento con un conjunto. Asimismo, se puede relacionar dos conjuntos definidos en un mismo universo. Los cuales se definen a continuación.

4.1 INCLUSIÓN DE CONJUNTOS

4.2 IGUALDAD DE CONJUNTOS

4.3 CONJUNTO DE PARTES

5. OPERACIONES ENTRE CONJUNTOS

Se combinan dos o más conjuntos mediantes reglas bien definidas para formar nuevos conjuntos. A esta combinación de conjuntos se le llaman operaciones entre los mismos, y son: unión, intersección, complementación, diferencia, diferencia simétrica y combinaciones de las mismas.

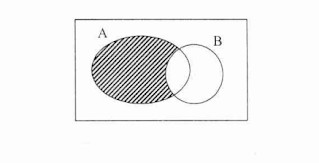
5.1 UNIÓN DE CONJUNTOS

La union de dos conjuntos ( AUB), se unen sus elementos.

Ejemplo:

A={a,e,i,u}

B={e,i,o,}

(AUB)={a,e,i,o,u}